Calculation of Equivalent Dihedral Angle
Introduction
Wing dihedral refers to the angle of wing panels as seen in the front view. The arrangement and amount of these angles determines in part the roll moment generated by the wing as a function of yaw angle. The dihedral of different wings can be quantified by a single value. Aerodynamicists quantify dihedral with the coefficient Cl� (Pronounced "see el beta"). Translated, this is the coefficient of roll moment due to yaw angle. Equivalent dihedral angle, EDA, is a similar measure that is more easily visualized. It is the dihedral angle of a V-dihedral wing with equivalent roll moment. Aerodynamicists do not use this term, although they may understand it. It is a simplification to say the EDA is constant for a given wing in all flight conditions, but it is a reasonable simplification.
EDA is a major factor in roll response, roll rate and spiral stability. For a rudder and elevator model at a given airspeed and yaw angle, the steady-state roll rate will be proportional to EDA. EDA is also one of three key factors in spiral stability (Reference 1).
This note describes how to calculate EDA for an unswept wing, the planform of which is reasonably elliptic.
Different Dihedral Schemes
Model airplanes use a variety of dihedral schemes. The most basic is V-dihedral. The dihedral angle of a V-dihedral wing is measured from the horizon to the wing, where both wings are at the same angle to the horizon.
"Polyhedral" wings break the wing up into two or more panels per semi-span. The dihedral angle for each panel is again measured to the horizon.
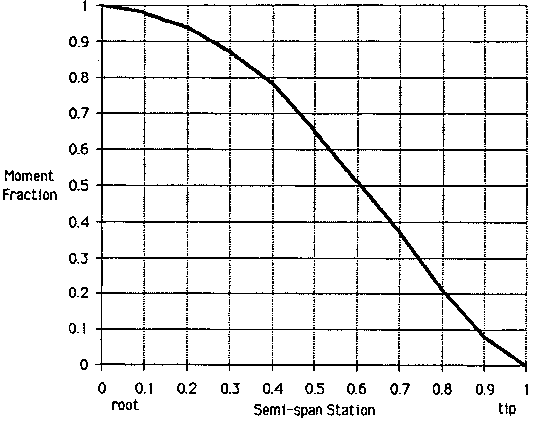
The figure above (from Reference 2) shows a curve relating the relative rolling moment of the wing as a function of the semi-span station. The basis is the moment at the root, or semi-span station zero. Thus, the relative rolling moment at station 0 is 1.0. This means that at the root the wing generates the full rolling moment.
Halfway out the wing at station 0.5, the wing generates 0.65 of the rolling moment. Even though less than half the wing area is outboard of station 0.5, it has a longer lever arm, so it generates nearly two-thirds of the rolling moment.
At station 0.8, the rolling moment is down to 0.2. Despite the long moment arm here, the much smaller area of the assumed elliptic planform tip cuts into the rolling moment. Planforms that are broader in the tip would have slightly more moment generated outboard.
Calculation of EDA
Calculation of EDA is straightforward. First locate the semi-span station of each dihedral break. Second, measure the dihedral of each panel. Then calculate the EDA of each panel alone as if it is the only panel with dihedral. Then add up all the panels to get the total EDA. By the way, do this only for one side of the airplane – the other side is assumed to be symmetrical!
This may be easiest to explain by example:
A wing with a dihedral break at 0.5 semi-span, with a flat center panel and tips bent up 15�:
The EDA of the inner panel is:
0�(1-0.65) = 0�
The EDA of the outer panel is:
15�(0.65-0) = 9.75�
The total EDA of the wing is:
0� + 9.75� = 9.75�
A wing with a dihedral break at 0.5 and 0.8 semi-span, with dihedral angles from inboard to outboard of 5�, 10� and 15�:
The EDA of the inner panel is:
5�(1-0.65) = 1.75�
The EDA of the middle panel is:
10�(0.65-0.20) = 4.50�
The EDA of the tip panel is:
15�(0.20-0) = 3.00�
The total EDA of the wing is:
1.75� + 4.50� + 3.00� = 9.25�
Perhaps it is clear by now that a wing with any number of panels can be calculated. Note also that the calculation of a V-dihedral wing EDA is trivial.
Conclusion
A wing can be quantified as being equivalent in dihedral effect to a V-dihedral wing dihedral angle, or Equivalent Dihedral Angle. This angle is easy to calculate approximately. This angle influences roll behavior and spiral stability.
References
- Beron-Rawdon, B. "Spiral Stability Augmentation with a Piezo-Electric Rate Gyroscope" in Michael Shellim’s R/C Soaring web site, rc-soar.com, January 2000.
- Beron-Rawdon, B. "Dihedral", Model Aviation Magazine, August through November 1988.
